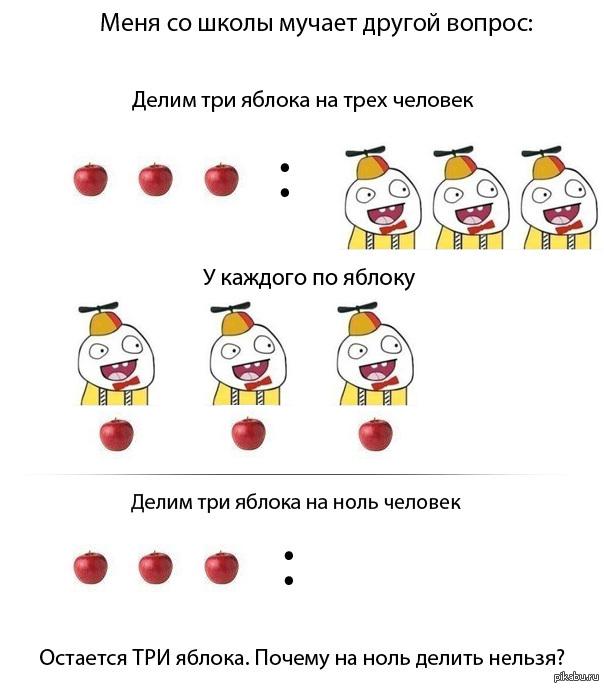
Miks me ei jaga nulliga?

Lugejad võivad küsida, miks ma pühendan nii banaalsele küsimusele terve artikli? Põhjuseks on jahmatav hulk üliõpilasi (!), kes juhuslikult nime all operatsiooni läbi viivad. Ja mitte ainult õpilased. Mõnikord püüan ja õpetajad. Millega selliste õpetajate õpilased matemaatikas hakkama saavad? Selle teksti kirjutamise vahetu põhjus oli vestlus õpetajaga, kelle jaoks nulliga jagamine polnud probleem ...

Nulliga jah, välja arvatud see, et üldse mitte millegi pärast, sest igapäevaelus pole meil seda tegelikult vaja kasutada. Me ei käi nullmunade pärast ostmas. “Ruumis on üks inimene” kõlab kuidagi loomulikult ja “null inimest” kõlab kunstlikult. Keeleteadlased ütlevad, et null on väljaspool keelesüsteemi.

Pangakontodel saame ka ilma nullita hakkama: kasutage – nagu termomeetril – punast ja sinist positiivsete ja negatiivsete väärtuste jaoks (pidage meeles, et temperatuuri puhul on loomulik kasutada punast positiivsete arvude jaoks ja pangakontode puhul seda on vastupidi, sest deebet peaks käivitama hoiatuse, nii et punane on väga soovitatav).

Kaasades naturaalarvuna nulli, puudutame diferentseerumise probleemi Kardinaalsed numbrid od majapidamine. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, … jooksul.

arvu võimsus on sama, mis selle koha number, kus see seisab. Muidu on see juba järjestuses 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, ....

Teisel kohal on üksikute komplektide arv, kolmandal kahe elemendiga komplektide arv jne. Peame selgitama, miks me näiteks sportlaste kohti võistlustel nullist ei nummerda. Siis saaks esikoha saanud hõbemedali (kuld läks nullkoha omanikule) jne. Mõnevõrra sarnast protseduuri kasutati jalgpallis – ma ei tea, kas Lugejad teavad, et "liiga üks" tähendab " parimat järgides." “ ja nullliigat kutsutakse saama „suurliigaks“.

Mõnikord kuuleme argumenti, et tuleb alustada nullist, sest IT-inimestele on see mugav. Neid kaalutlusi jätkates tuleks kilomeetri definitsiooni muuta - see peaks olema 1024 m, sest see on baitide arv kilobaidis (viitan arvutiteadlastele tuntud naljale: “Mis vahe on esmakursuslasel ja arvutiteaduse üliõpilane ja selle teaduskonna viienda kursuse tudeng? et kilobait on 1000 kilobaiti, viimane - et kilomeeter on 1024 meetrit")!

Teine seisukoht, mida tuleks juba tõsiselt võtta, on järgmine: mõõdame alati nullist! Piisab, kui vaadata joonlaual mis tahes skaalat, majapidamiskaalusid, isegi kella. Kuna mõõdame nullist ja loendamist võib mõista kui mõõtmist dimensioonita ühikuga, siis peaksime lugema nullist.

Asi on lihtne, aga...

Jätame üldise mõttekäigu ja naaseme nulliga jagamise juurde. Asi on lihtne ja see oleks lihtne, kui see poleks ... mis siis? Mõtleme ja proovime. Kui palju see võib olla – üks jagatud nulliga? Vaatame: 1/0 = x. Korrutage mõlemad pooled vasaku külje nimetajaga.

Saame 1=0. Midagi on valesti! Mis juhtus? Ah arvan! Eeldus, et on olemas ühtsuse ja nulli jagatis, viib vastuoluni. Ja kui ühte ei saa nulliga jagada, siis saab teist arvu. Kui, Lugeja, kehitad õlgu ja imestad, miks autor (see tähendab mina) sellistest tühisustest kirjutab, siis ... mul on väga hea meel!

Valemit 0/0 = 0 võiks kangekaelselt kaitsta, kuid see läheb vastuollu reegliga, et arvu endaga jagamise tulemus võrdub ühega. Absoluutselt, kuid üsna erinevad on arvutuses sellised sümbolid nagu 0/0, °/° jms. Need ei tähenda ühtegi numbrit, vaid on teatud tüüpi teatud jadade sümboolsed tähised.

Ühest elektrotehnika raamatust leidsin huvitava võrdluse: nulliga jagamine on sama ohtlik kui kõrgepingelekter. See on normaalne: Ohmi seadus ütleb, et pinge ja takistuse suhe on võrdne vooluga: V = U / R. Kui takistus oleks null, siis läbiks juhi teoreetiliselt lõpmatu vool, mis põletaks kõik võimalikud juhid.

Kunagi kirjutasin iga nädalapäeva kohta luuletuse nulliga jagamise ohtudest. Mäletan, et kõige dramaatilisem päev oli neljapäev, aga kahju on kogu mu tööst selles vallas.

Kui jagad midagi nulliga

Väga vara esmaspäeval

Nädal, mis just juhtus

Oled juba haledalt läbi kukkunud.

Kui teisipäeva pärastlõunal

Paned nimetajasse nulli

Ma ütlen sulle siis, sa eksid

Halb matemaatik!

Kui läbi nulli, läbi perverssuse,

Tahaks kolmapäeval lahku minna

Sa jääd palju hätta

Sul on hein ja vesi peas!

Üks Bartek oli meiega.

Ta oli reeglitega vastuolus.

Neljapäeval jagub see nulliga.

Ta ei ole enam meie vahel!

Kui imelik soov sind valdab

Reedel jagage nulliga

Ma ütlen ausalt, ma ütlen ausalt:

Halb algus sellele nädalavahetusele.

Kui on null, siis kuskil laupäeval

Jagaja on teie oma (mitte paksus kirjas)

Põlvita kirikuaia alla.

See on teie ülestõusmine.

Kas soovite kriipsu alla nulli,

Tee pühapäeval puhkus

Kaasa võtta kriit, must tahvel.

Kirjutage: see ei jagu nulliga!

Null on seotud tühjuse ja tühisusega. Tõepoolest, ta jõudis matemaatika juurde kui suuruseni, mis ühelegi liites seda ei muuda: x + 0 = x. Kuid nüüd on null mitmes teises väärtuses, eriti kui skaala algus. Kui väljaspool akent pole plusstemperatuuri ega härmatist, siis ... see on null, mis ei tähenda, et temperatuuri pole üldse. Nullklassi monument ei ole see, mida on ammu lammutatud ja mida lihtsalt pole. Vastupidi, see on midagi Waweli, Eiffeli torni ja Vabadussammas sarnast.

Noh, nulli tähtsust positsioonisüsteemis ei saa vaevalt üle hinnata. Kas sa tead, lugeja, mitu nulli on Bill Gatesil pangakontol? Ma ei tea, aga pool tahaks. Ilmselt märkas Napoleon Bonaparte, et inimesed on nagu nullid: nad omandavad tähenduse positsiooni kaudu. Andrzej Wajda filmis As the Years, As the Days Go by plahvatab kirglik kunstnik Jerzy: "Vilist on null, nihil, ei midagi, mitte midagi, nihil, null." Kuid null võib olla hea: "null kõrvalekalle normist" tähendab, et kõik läheb hästi, ja jätkake samamoodi!

Tuleme tagasi matemaatika juurde. Nulli saab karistamatult liita, lahutada ja korrutada. "Ma võtsin juurde null kilogrammi," ütleb Manya Anyale. "Ja see on huvitav, sest kaotasin sama kaalu," vastab Anya. Nii et sööme kuus korda kuus nullportsjonit jäätist, see ei tee meile halba.

Me ei saa nulliga jagada, küll aga saame jagada nulliga. Nullpelmeenide taldriku saab kergesti kätte ulatada neile, kes toidu ootavad. Kui palju igaüks saab?

Null ei ole positiivne ega negatiivne. See ja number mittepositiivneи mittenegatiivne. See rahuldab võrratused x≥0 ja x≤0. Vastuolu "midagi positiivset" ei ole "midagi negatiivset", vaid "midagi negatiivset või nulliga võrdset". Matemaatikud, vastupidiselt keelereeglitele, ütlevad alati, et miski on "võrdne nulliga" ja mitte "null". Selle praktika õigustamiseks on meil: kui loeme valemit x = 0 "x on null", siis x = 1 loeme "x on võrdne ühega", mille võiks alla neelata, aga kuidas on lood "x = 1534267"? Samuti ei saa te märgile 0 arvväärtust määrata⁰ega tõsta nulli negatiivseks astmeks. Teisest küljest võite suvaliselt juurutada nulli... ja tulemus on alati null. 

Eksponentfunktsioon y = a^x, a positiivne alus ei muutu kunagi nulliks. Sellest järeldub, et nulllogaritmi ei eksisteeri. Tõepoolest, a logaritm aluse b suhtes on eksponent, milleni tuleb alust tõsta, et saada a logaritm. Kui a = 0, sellist indikaatorit pole ja null ei saa olla logaritmi alus. Newtoni sümboli "nimetajas" olev null on aga midagi muud. Eeldame, et need kokkulepped ei too kaasa vastuolu.

valetõendid

Nulliga jagamine on valetõestuste tavaline teema ja seda juhtub isegi kogenud matemaatikutega. Lubage mul tuua teile kaks oma lemmiknäidet. Esimene on algebraline. Ma "tõestan", et kõik arvud on võrdsed. Oletame, et on kaks arvu, mis ei ole võrdsed. Seetõttu on üks neist suurem kui teine, olgu a > b. Oletame, et c on nende erinevus

c \uXNUMXd a - b. Seega on meil a - b = c, kust a = b + c.

Korrutame viimase mõlemad osad a - b-ga:

a² – ab = ab + ac – b2 – bc.

Tõlgin ak vasakule poole, muidugi mäletan märgi muutmist:

a² - ab - ac = ab - b2 - bc.

Ma välistan tavalised tegurid:

A (a-b-c) \uXNUMXd b (a-b-c),

Jagan ja mul on see, mida tahtsin:

a = b.

Ja tegelikult veel kummalisem, sest eeldasin, et a > b ja sain, et a = b. Kui ülaltoodud näites on "petmist" lihtne ära tunda, siis allolevas geomeetrilises tõestuses see nii lihtne ei ole. Ma tõestan, et ... trapetsi pole olemas. Figuuri, mida tavaliselt nimetatakse trapetsiks, ei eksisteeri.

Kuid oletame esmalt, et on olemas selline asi nagu trapets (ABCD alloleval joonisel). Sellel on kaks paralleelset külge ("alused"). Venitame need alused, nagu pildil näidatud, nii et saame rööpküliku. Selle diagonaalid jagavad trapetsi teise diagonaali segmentideks, mille pikkused on tähistatud x, y, z, nagu 1 joonis. Vastavate kolmnurkade sarnasusest saame proportsioonid:

kus me määratleme:

Oraz

kus me määratleme:

Lahutage tärnidega tähistatud võrdsuse küljed:

 Lühendades mõlemat külge x − z võrra, saame – a/b = 1, mis tähendab, et a + b = 0. Kuid arvud a, b on trapetsi aluste pikkused. Kui nende summa on null, siis on nemadki null. See tähendab, et sellist kujundit nagu trapets ei saa eksisteerida! Ja kuna ristkülikud, rombid ja ruudud on ka trapetsid, siis, kallis lugeja, pole ka rombusid, ristkülikuid ja ruute ...

Arva ära

Teabe jagamine on neljast põhitegevusest kõige huvitavam ja väljakutsuvam. Siin kohtame esimest korda täiskasvanueas nii levinud nähtust: "arvake vastus ära ja kontrollige siis, kas arvasite õigesti". Seda väljendab väga tabavalt Daniel K. Dennett (“Kuidas teha vigu?”, raamatus How It Is – A Scientific Guide to the Universe, CiS, Varssavi, 1997):

See "arvamisviis" ei sega meie täiskasvanuelu – võib-olla sellepärast, et me õpime selle varakult selgeks ja arvamine pole keeruline. Ideoloogiliselt esineb sama nähtus näiteks matemaatilises (täielikus) induktsioonis. Sealsamas “arvame ära” valemi ja siis kontrollime, kas meie oletus on õige. Õpilased küsivad alati: „Kuidas me mustrit teadsime? Kuidas seda välja võtta?" Kui õpilased mulle selle küsimuse esitavad, muudan nende küsimuse naljaks: "Ma tean seda, sest olen professionaal, sest mulle makstakse selle teadmise eest." Õpilastele koolis saab vastata samas stiilis, ainult et tõsisemalt.

Harjutus. Pange tähele, et liitmist ja kirjalikku korrutamist alustame madalaimast ühikust ning jagamist suurimast ühikust.

Kahe idee kombinatsioon

Matemaatikaõpetajad on alati juhtinud tähelepanu sellele, et see, mida me nimetame täiskasvanute eraldamiseks, on kahe kontseptuaalselt erineva idee liit: Корпус i eraldamine.

Esimene (Корпус) esineb ülesannetes, mille arhetüüp on:

Jaga-jaga Need on sellised ülesanded nagu:

? (Säilitame selle probleemi algse stiili, mis on võetud 1892. aastal Krakowis avaldatud Julian Zgozalewiczi käsiraamatust – zlot on Reini zlott, valuuta, mis oli Austria-Ungari impeeriumis käibel kuni XNUMX. sajandi alguseni).

Nüüd kaaluge kahte probleemi vanim poolakeelne matemaatikaõpik, isa Tomasz Clos (1538). Kas see on diviis või kupee? Lahendage see nii, nagu peaksid XNUMX. sajandi koolilapsed:

(Tõlge poola keelest poola keelde: vaadis on kvart ja neli potti. Pott on neli liitrit. Keegi ostis kaubanduseks 20 vaadi veini 50 zł eest. Tollimaks ja maks (aktsiis?) tuleb 8 zł. Kui palju müüa liitrit, et teenida 8 zł?)

Sport, füüsika, kongruents

Vahel tuleb spordis midagi nulliga jagada (väravate suhe). Eks kohtunikud kuidagi saavad sellega hakkama. Abstraktses algebras on need aga päevakorras. nullist erinevad kogusedmille ruut on null. Seda võib isegi lihtsalt seletada.

Vaatleme funktsiooni F, mis seob punkti (y, 0) punktiga tasandis (x, y). Mis on F², see tähendab F topelttäitmist? Nullfunktsioon – igal punktil on pilt (0,0).

Lõpuks on nullist erinevad suurused, mille ruut on 0, füüsikute jaoks peaaegu igapäevane leib ja arvud kujul a + bε, kus ε ≠ 0, aga ε² = 0, helistavad matemaatikud topeltnumbrid. Need esinevad matemaatilises analüüsis ja diferentsiaalgeomeetrias.

Lõppude lõpuks on aritmeetikas midagi, mille nimi jagab nulliga. See pärineb kokkulangevus. Olgu Z tähistab täisarvude hulka. Hulga Z jagamine p-ga tähendab, et võrdsustame iga arvu (täisarvu) mõne teisega, nimelt nendega, millega nende erinevus jagub. Seega, kui meil on viit tüüpi numbreid, mis vastavad numbritele 0, 1, 2, 3, 4 - võimalikud jäägid, kui need jagatakse 5-ga. Valem on kirjutatud järgmiselt:

mod, kui erinevus on mitmekordne.

= 2 puhul on meil ainult kaks arvu: 0 ja 1. Täisarvude jagamine kahte sellisesse klassi võrdub nende jagamisega paaris- ja paarituteks. Asendame selle kohe. Erinevus jagub alati 1-ga (iga täisarv jagub 1-ga). Kas on võimalik võtta =0? Proovime: millal on kahe arvu erinevus nulli kordne? Ainult siis, kui need kaks arvu on võrdsed. Seega on täisarvude hulga nulliga jagamine mõttekas, kuid see pole huvitav: midagi ei juhtu. Siiski tuleb rõhutada, et see ei ole arvude jagamine algkoolist tuntud tähenduses.

Sellised tegevused on lihtsalt keelatud, nagu ka pikk ja lai matemaatika.

Riis. 2. Numbrite tuvastamine võrdluse abil

(režiim 5 ja režiim 2)